How to Write an Equation for a Graph Parent Functions

2.5 Using Transformations to Graph Functions

Learning Objectives

1. Define the rigid transformations and use them to sketch graphs.
2. Define the non-rigid transformations and use them to sketch graphs.

Vertical and Horizontal Translations

When the graph of a function is changed in appearance and/or location we call it a transformation. There are two types of transformations. A rigid transformationA set of operations that change the location of a graph in a coordinate plane but leave the size and shape unchanged. changes the location of the function in a coordinate plane, but leaves the size and shape of the graph unchanged. A non-rigid transformationA set of operations that change the size and/or shape of a graph in a coordinate plane. changes the size and/or shape of the graph.

A vertical translationA rigid transformation that shifts a graph up or down. is a rigid transformation that shifts a graph up or down relative to the original graph. This occurs when a constant is added to any function. If we add a positive constant to each y-coordinate, the graph will shift up. If we add a negative constant, the graph will shift down. For example, consider the functions $g(x)=x^2-3$ and $h(x)=x^2+3.$ Begin by evaluating for some values of the independent variable x.

Now plot the points and compare the graphs of the functions g and h to the basic graph of $f(x)=x^2$ , which is shown using a dashed grey curve below.

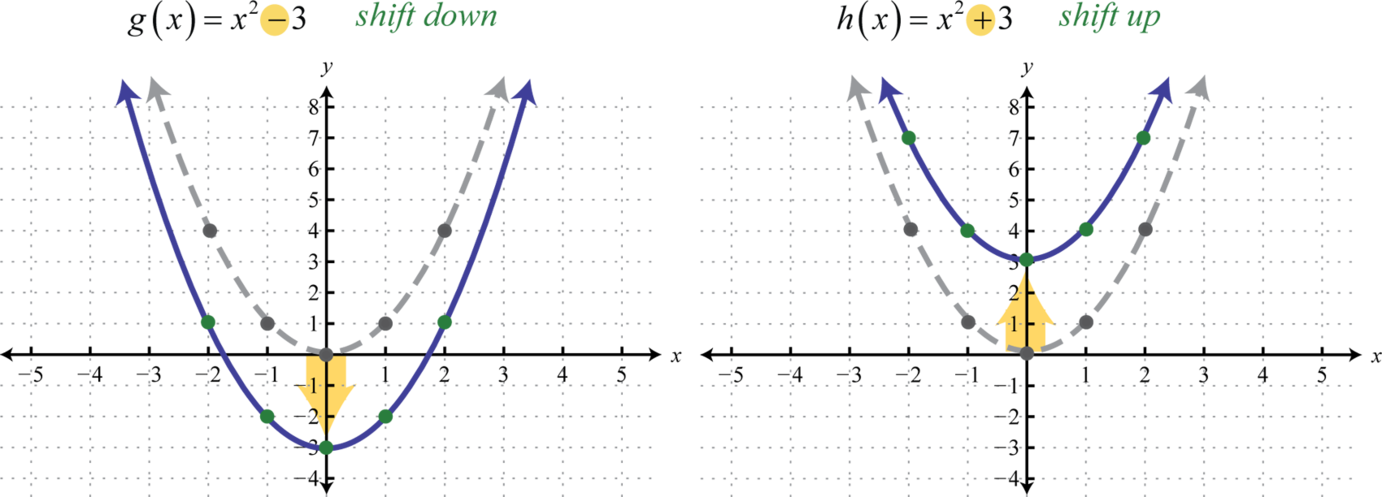
The function g shifts the basic graph down 3 units and the function h shifts the basic graph up 3 units. In general, this describes the vertical translations; if k is any positive real number:

Vertical shift up k units:	$F(x)=f(x)+k$
Vertical shift down k units:	$F(x)=f(x)-k$

Example 1

Sketch the graph of $g(x)=\sqrt{x}+4.$

Solution:

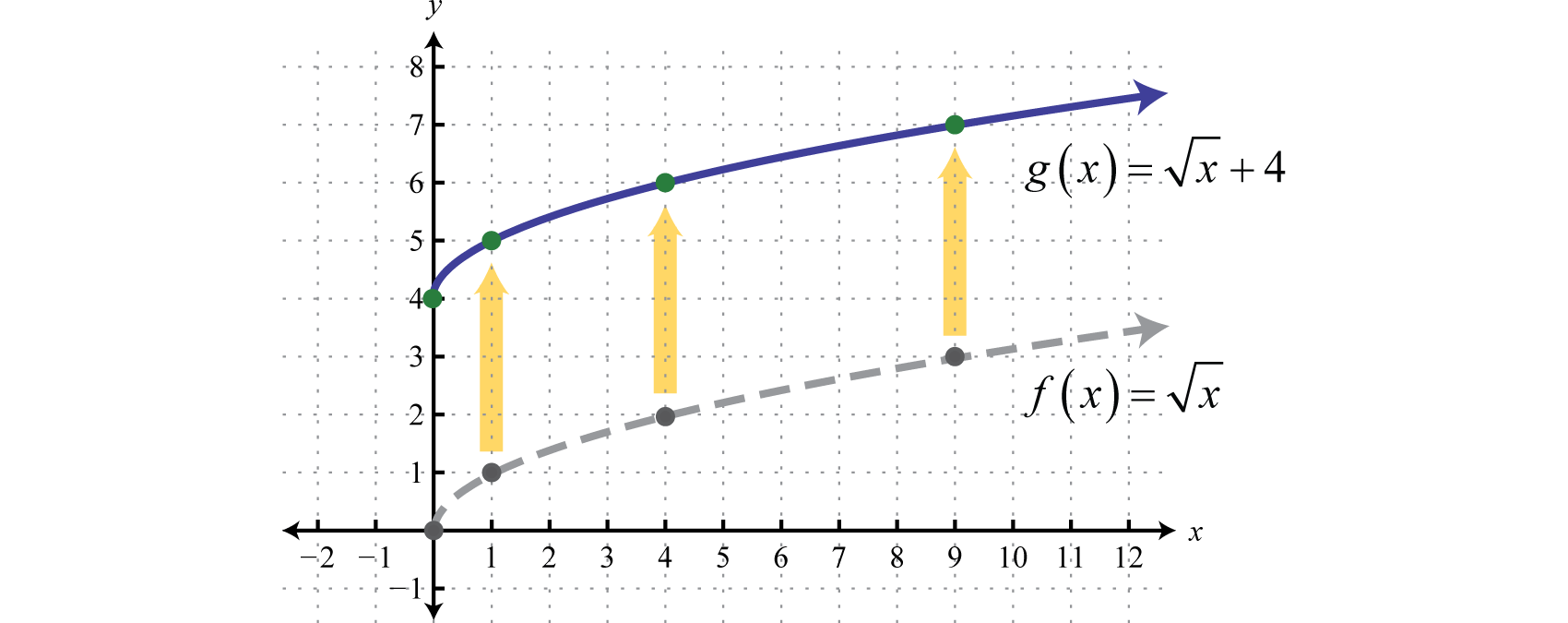
Begin with the basic function defined by $f(x)=\sqrt{x}$ and shift the graph up 4 units.

Answer:

A horizontal translationA rigid transformation that shifts a graph left or right. is a rigid transformation that shifts a graph left or right relative to the original graph. This occurs when we add or subtract constants from the x-coordinate before the function is applied. For example, consider the functions defined by $g(x)={(x+3)}^2$ and $h(x)={(x-3)}^2$ and create the following tables:

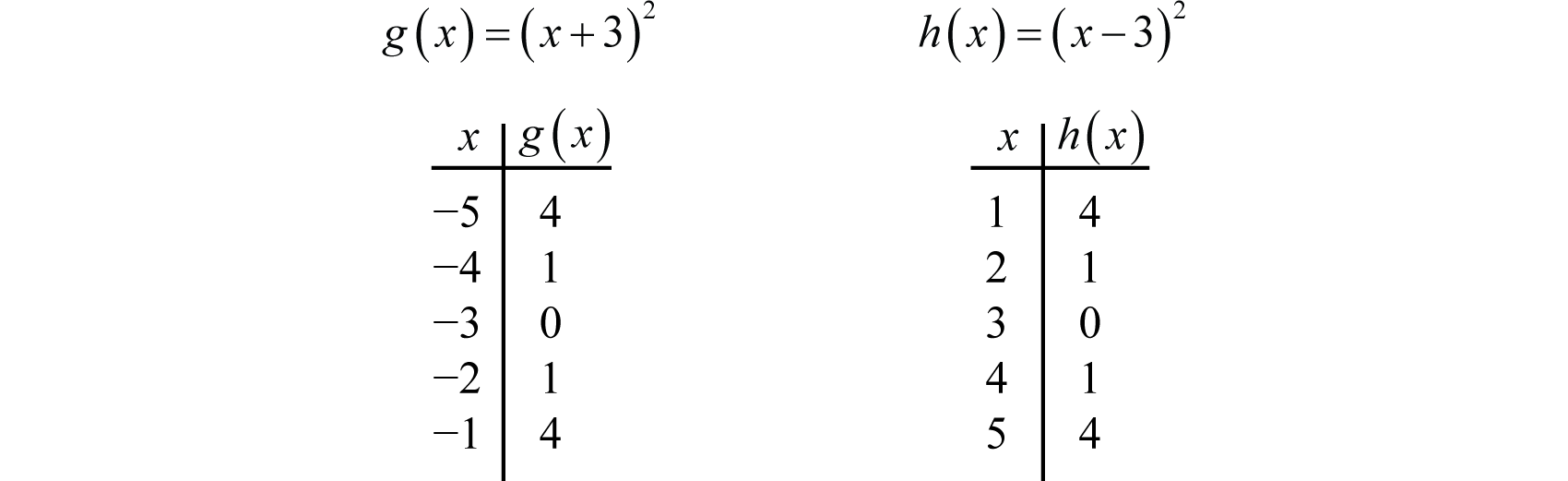
Here we add and subtract from the x-coordinates and then square the result. This produces a horizontal translation.

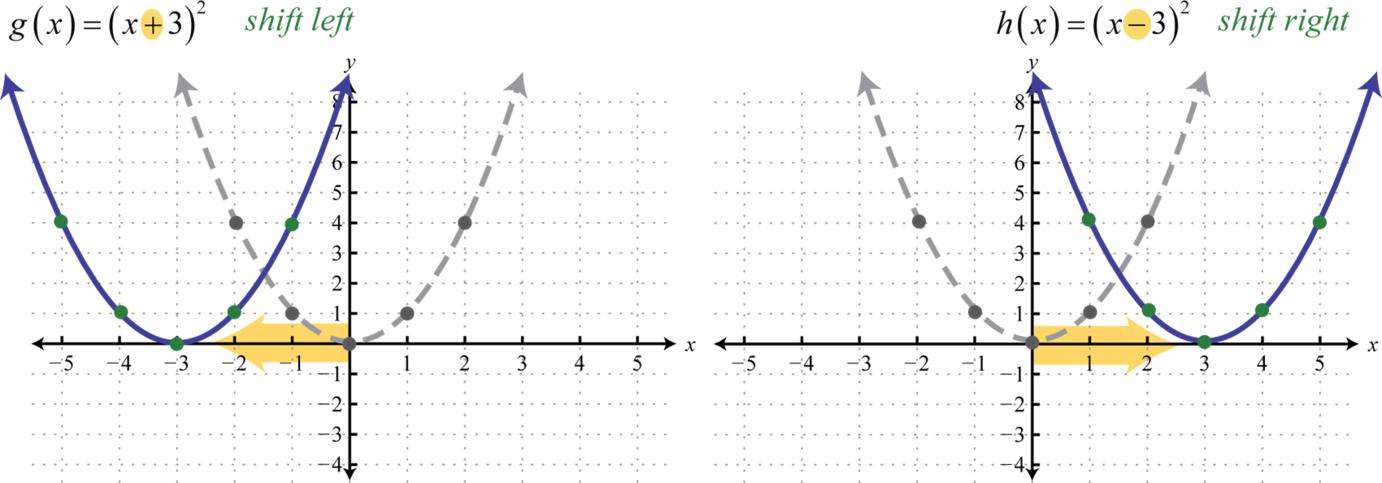
Note that this is the opposite of what you might expect. In general, this describes the horizontal translations; if h is any positive real number:

Horizontal shift left h units:	$F(x)=f(x+h)$
Horizontal shift right h units:	$F(x)=f(x-h)$

Example 2

Sketch the graph of $g(x)={(x-4)}^3.$

Solution:

Begin with a basic cubing function defined by $f(x)=x^3$ and shift the graph 4 units to the right.

Answer:

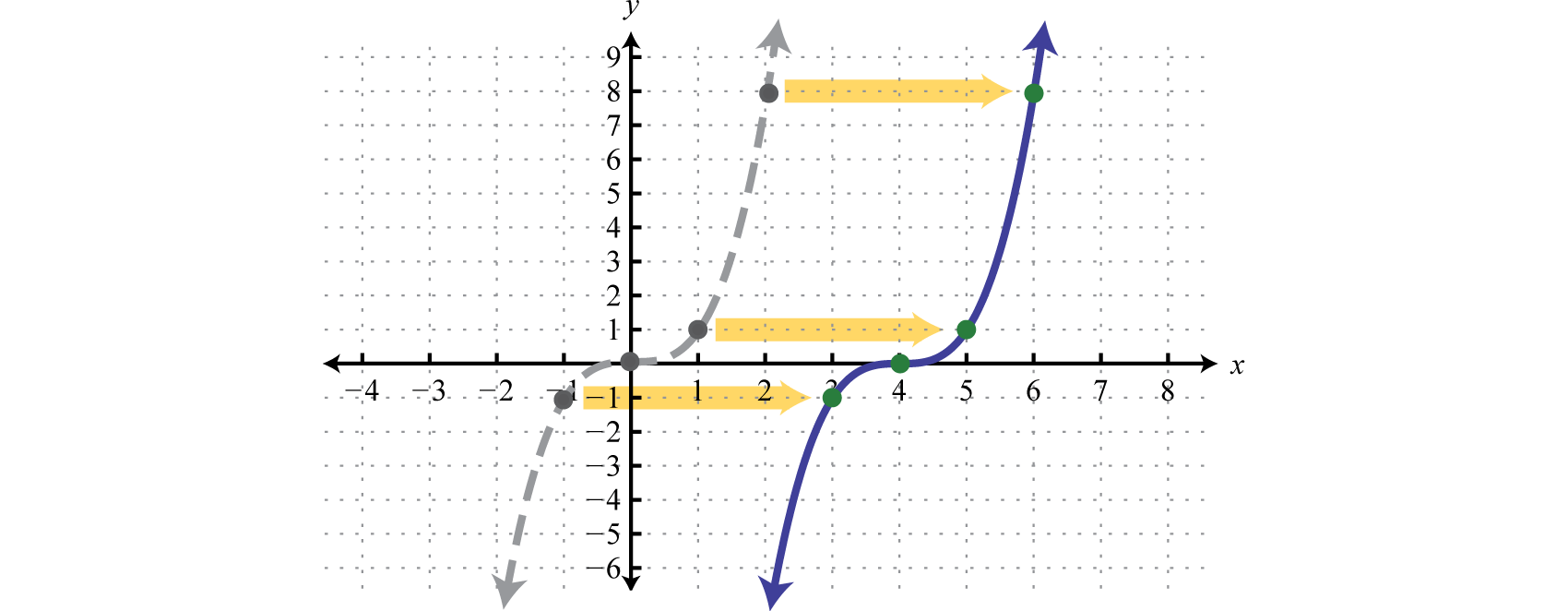
It is often the case that combinations of translations occur.

Example 3

Sketch the graph of $g(x)=|x+3|-5.$

Solution:

Start with the absolute value function and apply the following transformations.

$$\begin{array}{llll}y\hfill & =\hfill & \left|x\right|\hfill & Basicfunction\hfill \\ y\hfill & =\hfill & |x+3|\hfill & Horizontalshiftleft3units\hfill \\ y\hfill & =\hfill & |x+3|-5\hfill & Verticalshiftdown5units\hfill \end{array}$$

Answer:

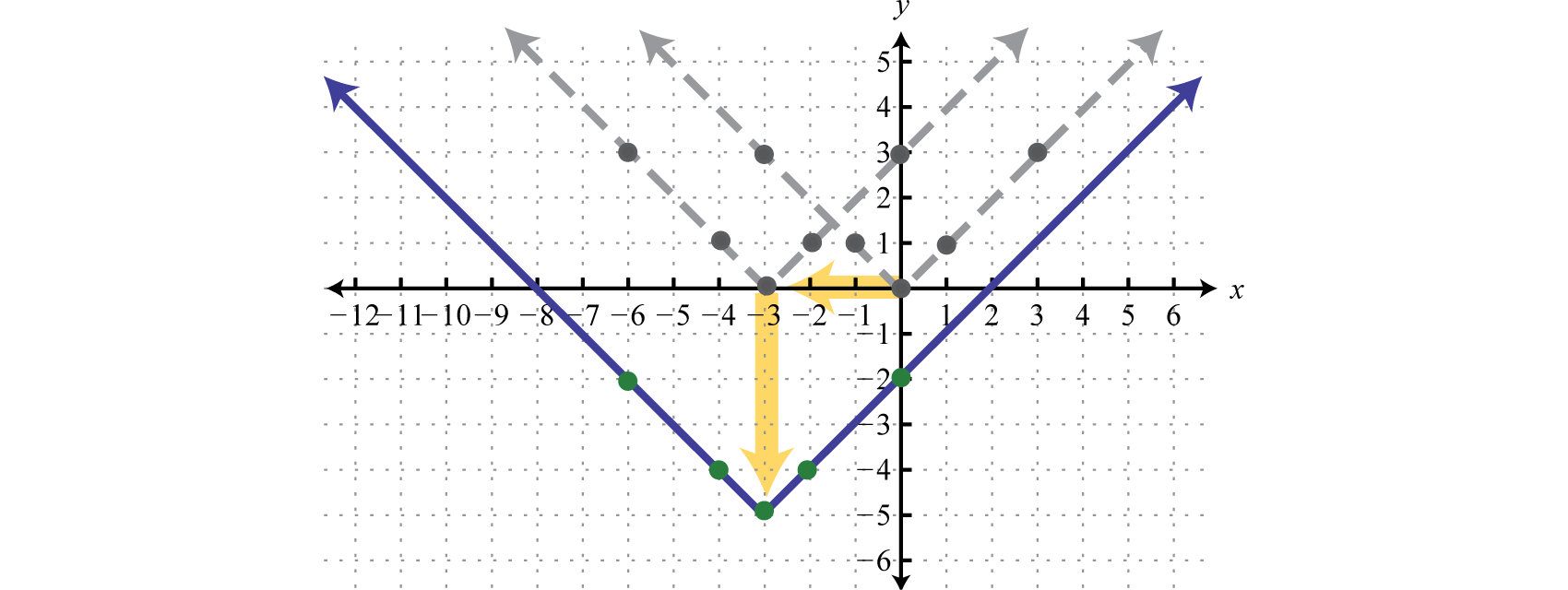
The order in which we apply horizontal and vertical translations does not affect the final graph.

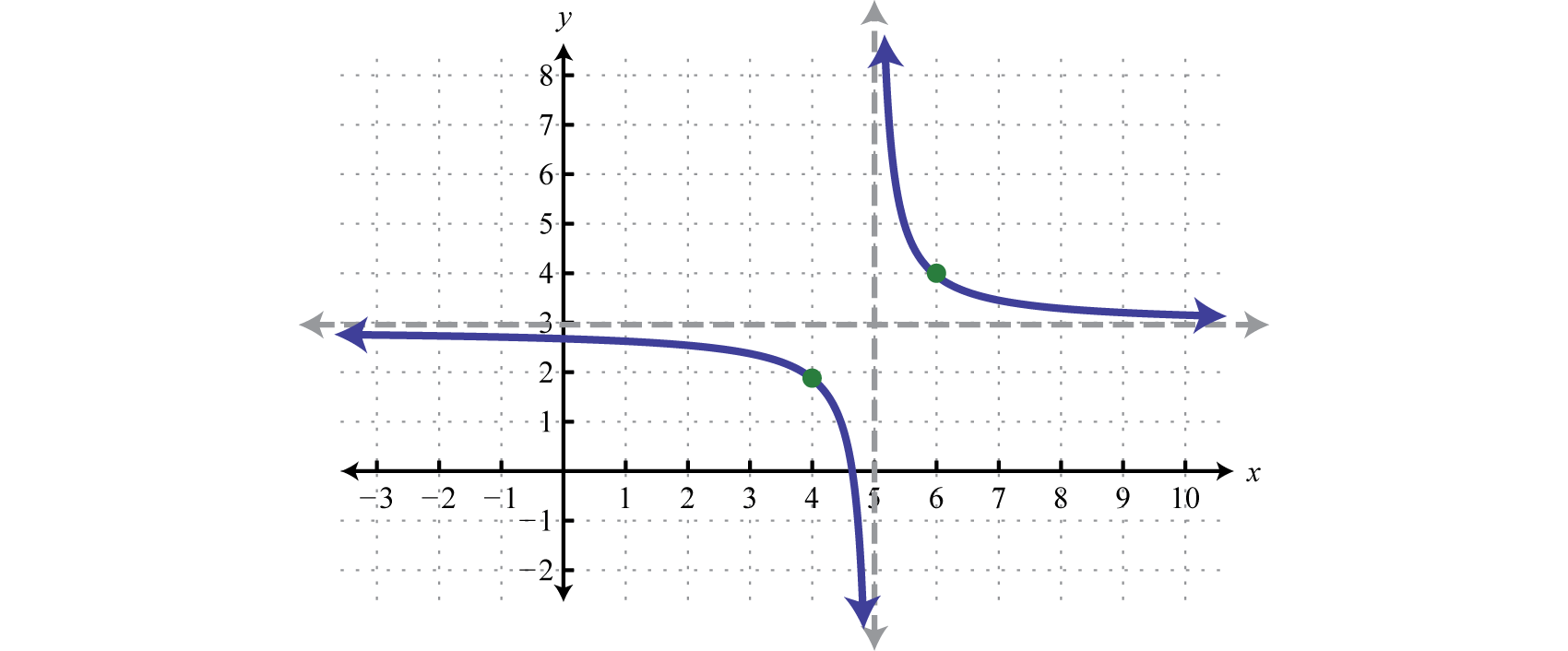
Example 4

Sketch the graph of $g(x)=\frac{1}{x-5}+3.$

Solution:

Begin with the reciprocal function and identify the translations.

$$\begin{array}{llll}y\hfill & =\hfill & \frac{1}{x}\hfill & Basicfunction\hfill \\ y\hfill & =\hfill & \frac{1}{x-5}\hfill & Horizontalshiftright5units\hfill \\ y\hfill & =\hfill & \frac{1}{x-5}+3\hfill & Verticalshiftup3units\hfill \end{array}$$

Take care to shift the vertical asymptote from the y-axis 5 units to the right and shift the horizontal asymptote from the x-axis up 3 units.

Answer:

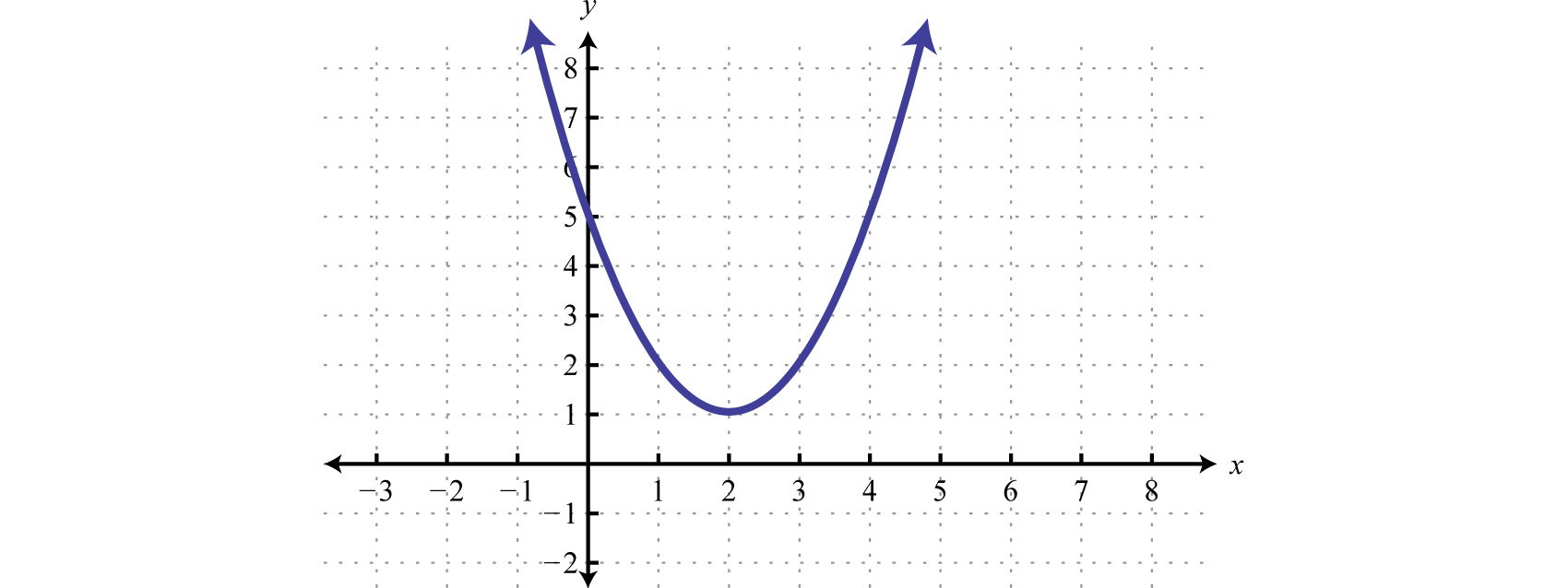
Try this! Sketch the graph of $g(x)={(x-2)}^2+1.$

Answer:

Reflections

A reflectionA transformation that produces a mirror image of the graph about an axis. is a transformation in which a mirror image of the graph is produced about an axis. In this section, we will consider reflections about the x- and y-axis. The graph of a function is reflected about the x-axis if each y-coordinate is multiplied by −1. The graph of a function is reflected about the y-axis if each x-coordinate is multiplied by −1 before the function is applied. For example, consider $g(x)=\sqrt{-x}$ and $h(x)=-\sqrt{x}.$

Compare the graph of g and h to the basic square root function defined by $f(x)=\sqrt{x}$ , shown dashed in grey below:

The first function g has a negative factor that appears "inside" the function; this produces a reflection about the y-axis. The second function h has a negative factor that appears "outside" the function; this produces a reflection about the x-axis. In general, it is true that:

Reflection about the y-axis:	$F(x)=f(-x)$
Reflection about the x-axis:	$F(x)=-f(x)$

When sketching graphs that involve a reflection, consider the reflection first and then apply the vertical and/or horizontal translations.

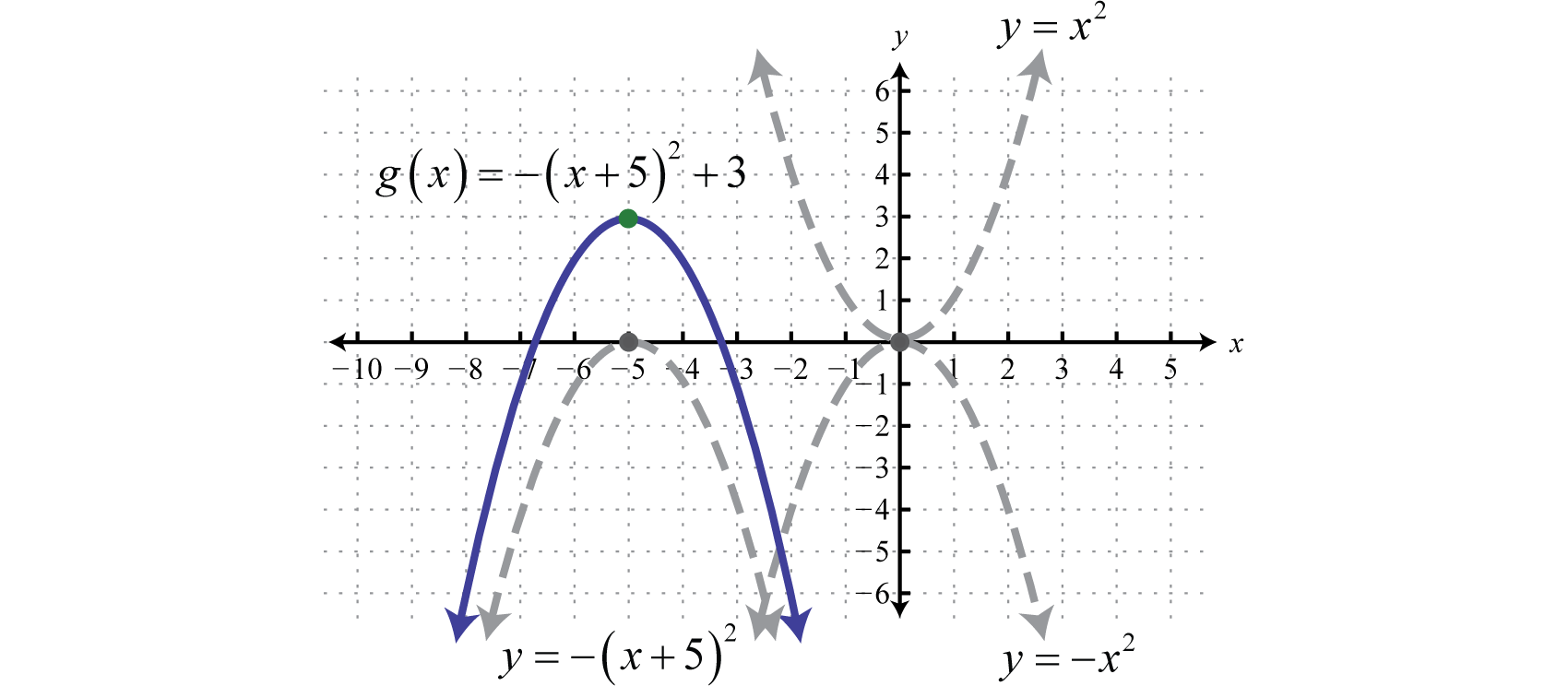
Example 5

Sketch the graph of $g(x)=-{(x+5)}^2+3.$

Solution:

Begin with the squaring function and then identify the transformations starting with any reflections.

$$\begin{array}{llll}y\hfill & =\hfill & x^2\hfill & Basicfunction.\hfill \\ y\hfill & =\hfill & -x^2\hfill & Reflectionaboutthex\text{-}axis.\hfill \\ y\hfill & =\hfill & -{(x+5)}^2\hfill & Horizontalshiftleft5units.\hfill \\ y\hfill & =\hfill & -{(x+5)}^2+3\hfill & Verticalshiftup3units.\hfill \end{array}$$

Use these translations to sketch the graph.

Answer:

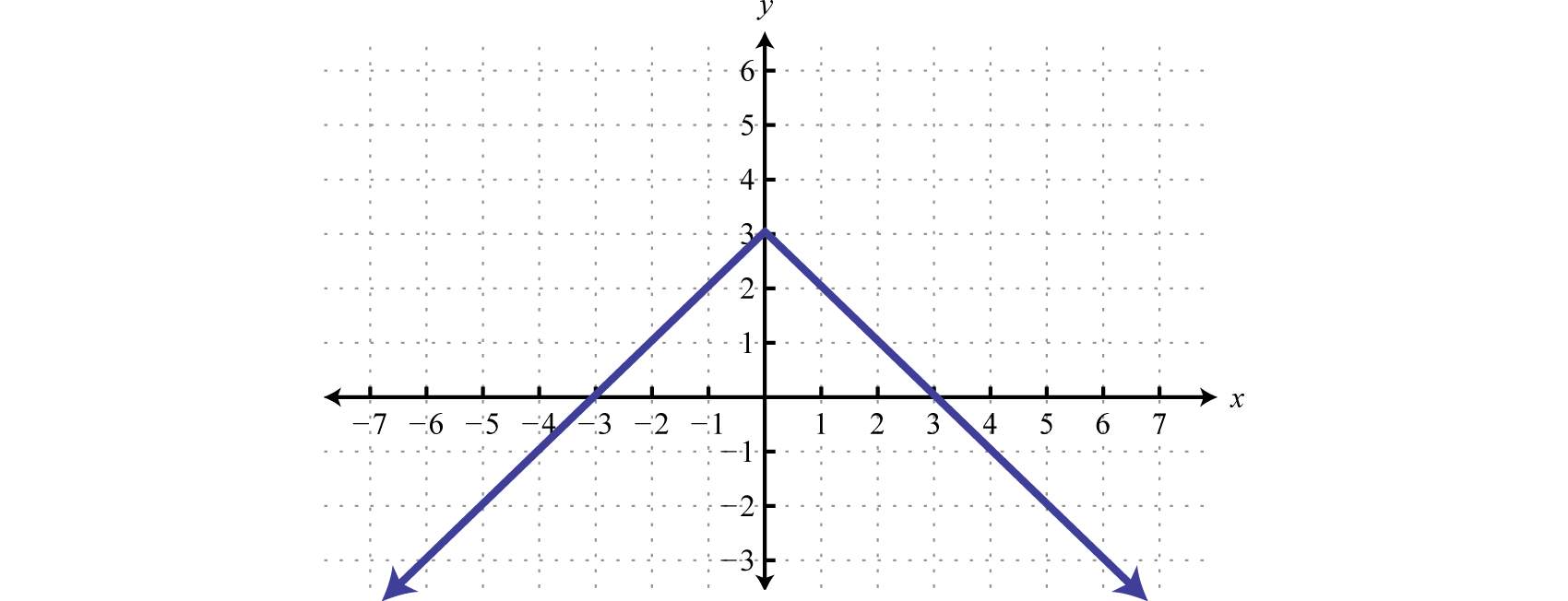
Try this! Sketch the graph of $g(x)=-\left|x\right|+3.$

Answer:

Dilations

Horizontal and vertical translations, as well as reflections, are called rigid transformations because the shape of the basic graph is left unchanged, or rigid. Functions that are multiplied by a real number other than 1, depending on the real number, appear to be stretched vertically or stretched horizontally. This type of non-rigid transformation is called a dilationA non-rigid transformation, produced by multiplying functions by a nonzero real number, which appears to stretch the graph either vertically or horizontally. . For example, we can multiply the squaring function $f(x)=x^2$ by 4 and $\frac{1}{4}$ to see what happens to the graph.

Compare the graph of g and h to the basic squaring function defined by $f(x)=x^2$ , shown dashed in grey below:

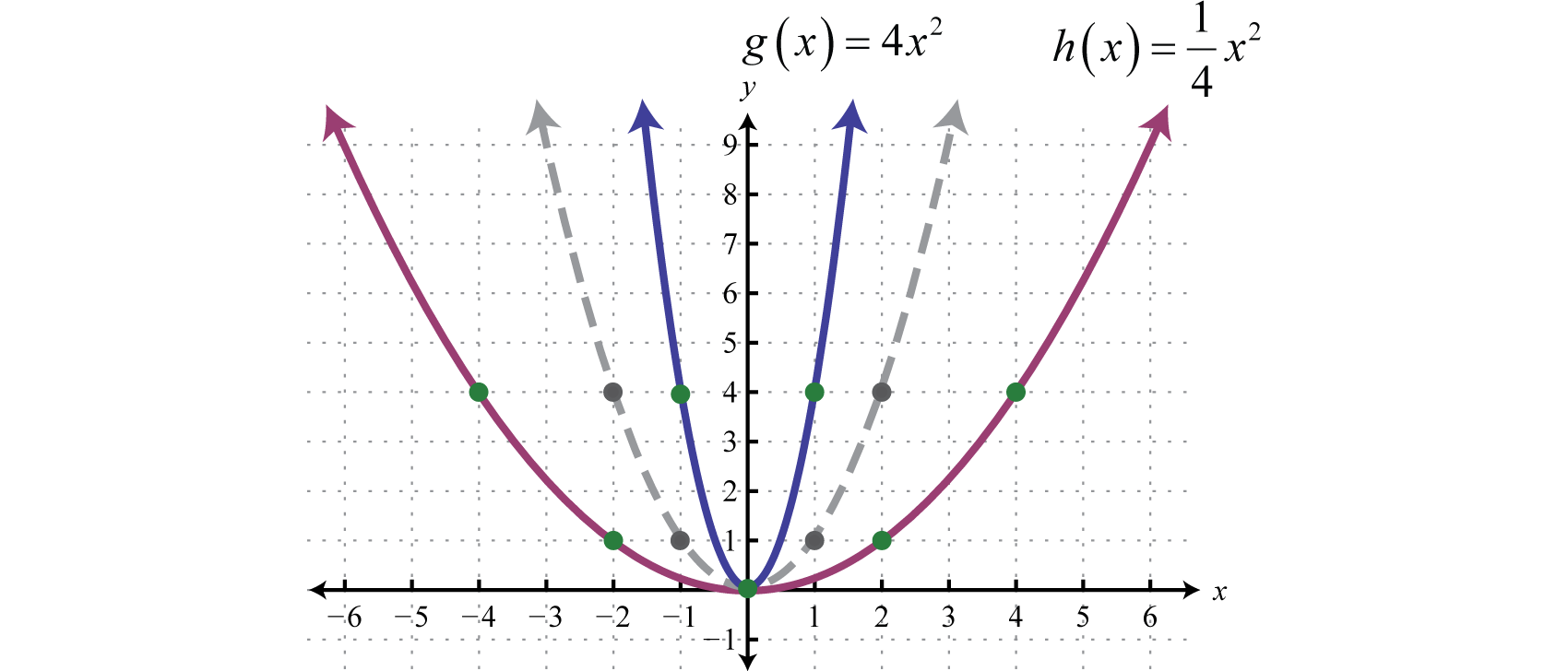
The function g is steeper than the basic squaring function and its graph appears to have been stretched vertically. The function h is not as steep as the basic squaring function and appears to have been stretched horizontally.

In general, we have:

If the factor a is a nonzero fraction between −1 and 1, it will stretch the graph horizontally. Otherwise, the graph will be stretched vertically. If the factor a is negative, then it will produce a reflection as well.

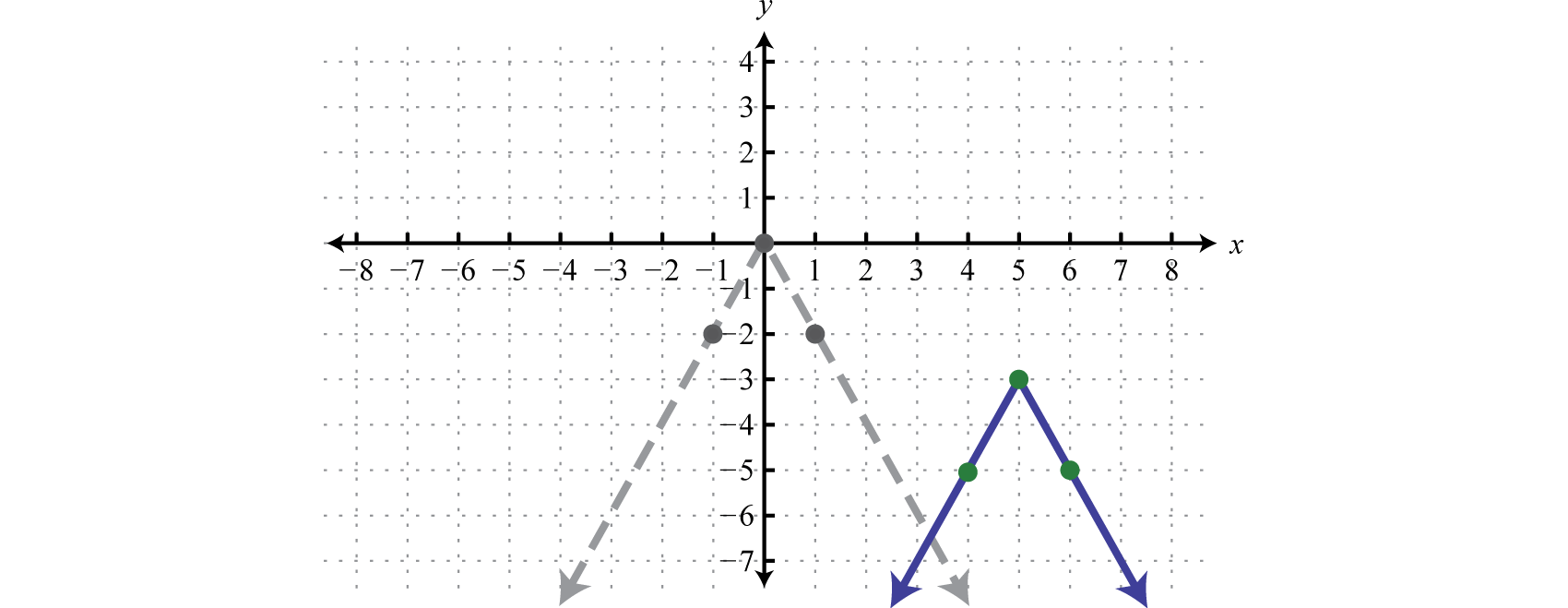
Example 6

Sketch the graph of $g(x)=-2|x-5|-3.$

Solution:

Here we begin with the product of −2 and the basic absolute value function: $y=-2\left|x\right|.$ This results in a reflection and a dilation.

$$\begin{array}{lll}\hfill x\hfill & \hfill y\hfill & y=-2\left|x\right|\leftarrow Dilationandreflection\hfill \\ \hfill -1& \hfill -2& y=-2|-1|=-2\cdot 1=-2\hfill \\ \hfill 0& \hfill 0& y=-2\left|0\right|=-2\cdot 0=0\hfill \\ \hfill 1& \hfill -2& y=-2\left|1\right|=-2\cdot 1=-2\hfill \end{array}$$

Use the points {(−1, −2), (0, 0), (1, −2)} to graph the reflected and dilated function $y=-2\left|x\right|.$ Then translate this graph 5 units to the right and 3 units down.

$$\begin{array}{llll}\hfill y& =\hfill & -2\left|x\right|\hfill & Basicgraphwithdilationand\hfill \\ \hfill & \hfill & \hfill & reflectionaboutthex-axis.\hfill \\ \hfill y& =\hfill & -2|x-5|\hfill & Shiftright5units.\hfill \\ \hfill y& =\hfill & -2|x-5|-3\hfill & Shiftdown3units.\hfill \end{array}$$

Answer:

In summary, given positive real numbers h and k:

Vertical shift up k units:	$F(x)=f(x)+k$
Vertical shift down k units:	$F(x)=f(x)-k$

Horizontal shift left h units:	$F(x)=f(x+h)$
Horizontal shift right h units:	$F(x)=f(x-h)$

Reflection about the y-axis:	$F(x)=f(-x)$
Reflection about the x-axis:	$F(x)=-f(x)$

Key Takeaways

• Identifying transformations allows us to quickly sketch the graph of functions. This skill will be useful as we progress in our study of mathematics. Often a geometric understanding of a problem will lead to a more elegant solution.
• If a positive constant is added to a function, $f(x)+k$ , the graph will shift up. If a positive constant is subtracted from a function, $f(x)-k$ , the graph will shift down. The basic shape of the graph will remain the same.
• If a positive constant is added to the value in the domain before the function is applied, $f(x+h)$ , the graph will shift to the left. If a positive constant is subtracted from the value in the domain before the function is applied, $f(x-h)$ , the graph will shift right. The basic shape will remain the same.
• Multiplying a function by a negative constant, $-f(x)$ , reflects its graph in the x-axis. Multiplying the values in the domain by −1 before applying the function, $f(-x)$ , reflects the graph about the y-axis.
• When applying multiple transformations, apply reflections first.
• Multiplying a function by a constant other than 1, $a\cdot f(x)$ , produces a dilation. If the constant is a positive number greater than 1, the graph will appear to stretch vertically. If the positive constant is a fraction less than 1, the graph will appear to stretch horizontally.

Topic Exercises

Part A: Vertical and Horizontal Translations

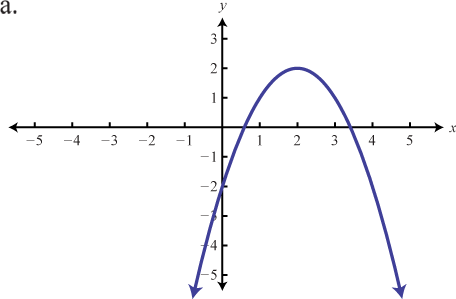
Match the graph to the function definition.













1. $f(x)=\sqrt{x+4}$

2. $f(x)=|x-2|-2$

3. $f(x)=\sqrt{x+1}-1$

4. $f(x)=|x-2|+1$

5. $f(x)=\sqrt{x+4}+1$

6. $f(x)=|x+2|-2$

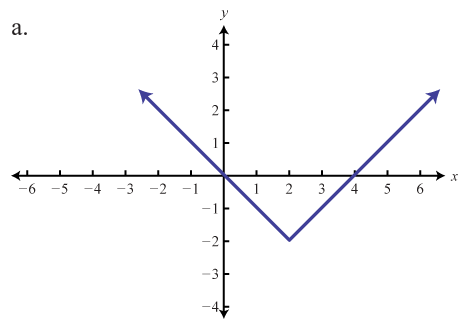
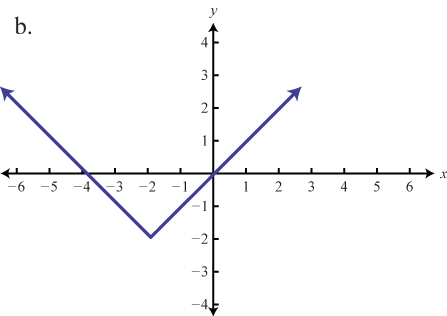
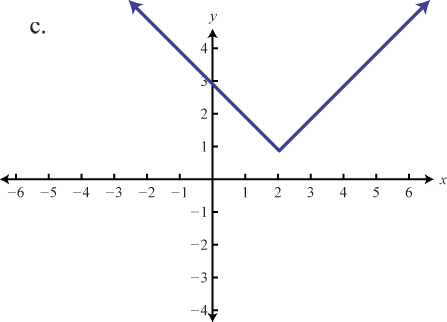
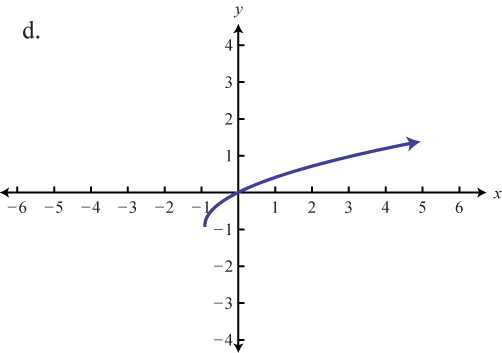
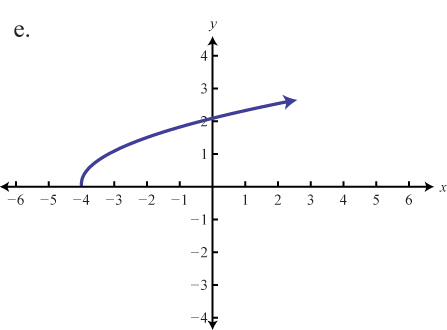
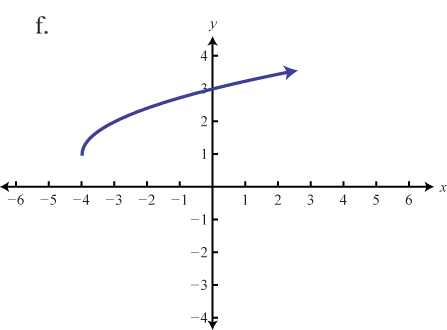
Graph the given function. Identify the basic function and translations used to sketch the graph. Then state the domain and range.

7. $f(x)=x+3$

8. $f(x)=x-2$

9. $g(x)=x^2+1$

10. $g(x)=x^2-4$

11. $g(x)={(x-5)}^2$

12. $g(x)={(x+1)}^2$

13. $g(x)={(x-5)}^2+2$

14. $g(x)={(x+2)}^2-5$

15. $h(x)=|x+4|$

16. $h(x)=|x-4|$

17. $h(x)=|x-1|-3$

18. $h(x)=|x+2|-5$

19. $g(x)=\sqrt{x}-5$

20. $g(x)=\sqrt{x-5}$

21. $g(x)=\sqrt{x-2}+1$

22. $g(x)=\sqrt{x+2}+3$

23. $h(x)={(x-2)}^3$

24. $h(x)=x^3+4$

25. $h(x)={(x-1)}^3-4$

26. $h(x)={(x+1)}^3+3$

27. $f(x)=\frac{1}{x-2}$

28. $f(x)=\frac{1}{x+3}$

29. $f(x)=\frac{1}{x}+5$

30. $f(x)=\frac{1}{x}-3$

31. $f(x)=\frac{1}{x+1}-2$

32. $f(x)=\frac{1}{x-3}+3$

33. $g(x)=-4$

34. $g(x)=2$

35. $f(x)=\sqrt[3]{x-2}+6$

36. $f(x)=\sqrt[3]{x+8}-4$

Graph the piecewise functions.

37. $$h(x)=\{\begin{array}{l}{x}^2+2\text{if}x<0\\ x+2\text{if}x\ge 0\end{array}$$

38. $$h(x)=\{\begin{array}{l}{x}^2-3\text{if}x<0\\ \sqrt{x}-3\text{if}x\ge 0\end{array}$$

39. $$h(x)=\{\begin{array}{l}{x}^3-1\text{if}x<0\\ |x-3|-4\text{if}x\ge 0\end{array}$$

40. $$h(x)=\{\begin{array}{lll}\hfill x^3& \text{if}\hfill & x<0\hfill \\ \hfill {(x-1)}^2-1& \text{if}\hfill & x\ge 0\hfill \end{array}$$

41. $$h(x)=\{\begin{array}{l}{x}^2-1\text{if}x<0\\ 2\text{if}x\ge 0\end{array}$$

42. $$h(x)=\{\begin{array}{lll}x+2\hfill & \text{if}\hfill & x<0\hfill \\ {(x-2)}^2\hfill & \text{if}\hfill & x\ge 0\hfill \end{array}$$

43. $$h(x)=\{\begin{array}{l}{\left(x+10\right)}^2-4\text{if}x<-8\\ x+4\text{if}-8\le x<-4\\ \sqrt{x+4}\text{if}x\ge -4\end{array}$$

44. $$f(x)=\{\begin{array}{l}x+10\text{if}x\le -10\\ |x-5|-15\text{if}-10<x\le 20\\ 10\text{if}x>20\end{array}$$

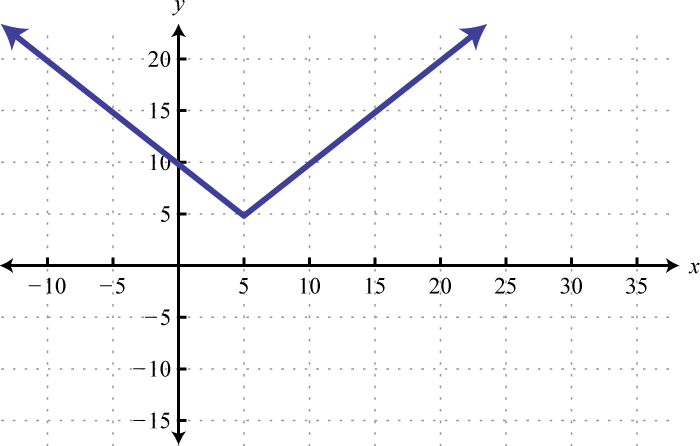
Write an equation that represents the function whose graph is given.

45. 

46. 

47. 

48. 

49. 

50. 

51. 

52. 

Part B: Reflections and Dilations

Match the graph the given function definition.













53. $f(x)=-3\left|x\right|$

54. $f(x)=-{(x+3)}^2-1$

55. $f(x)=-|x+1|+2$

56. $f(x)=-x^2+1$

57. $f(x)=-\frac{1}{3}\left|x\right|$

58. $f(x)=-{(x-2)}^2+2$

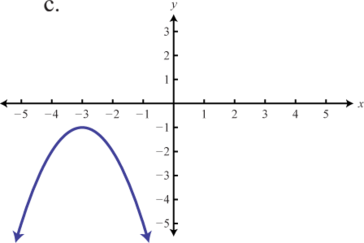
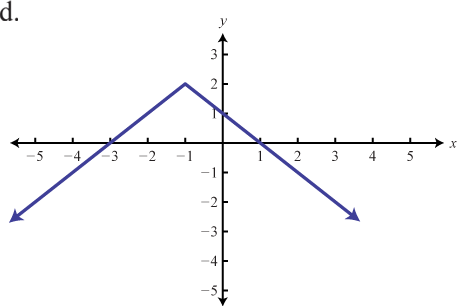
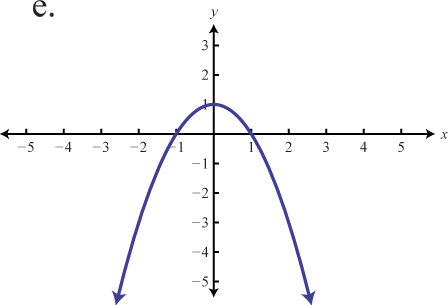
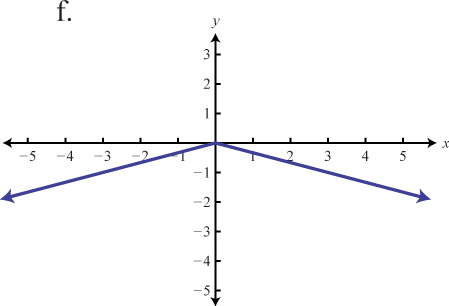
Use the transformations to graph the following functions.

59. $f(x)=-x+5$

60. $f(x)=-\left|x\right|-3$

61. $g(x)=-|x-1|$

62. $f(x)=-{(x+2)}^2$

63. $h(x)=\sqrt{-x}+2$

64. $g(x)=-\sqrt{x}+2$

65. $g(x)=-(x+2{)}^3$

66. $h(x)=-\sqrt{x-2}+1$

67. $g(x)=-x^3+4$

68. $f(x)=-x^2+6$

69. $f(x)=-3\left|x\right|$

70. $g(x)=-2x^2$

71. $h(x)=\frac{1}{2}(x-1{)}^2$

72. $h(x)=\frac{1}{3}(x+2{)}^2$

73. $g(x)=-\frac{1}{2}\sqrt{x-3}$

74. $f(x)=-5\sqrt{x+2}$

75. $f(x)=4\sqrt{x-1}+2$

76. $h(x)=-2x+1$

77. $g(x)=-\frac{1}{4}(x+3{)}^3-1$

78. $f(x)=-5(x-3{)}^2+3$

79. $h(x)=-3|x+4|-2$

80. $f(x)=-\frac{1}{x}$

81. $f(x)=-\frac{1}{x+2}$

82. $f(x)=-\frac{1}{x+1}+2$

Part C: Discussion Board

83. Use different colors to graph the family of graphs defined by $y=k{x}^2$ , where $k\in \left\{1,\frac{1}{2},\frac{1}{3},\frac{1}{4}\right\}.$ What happens to the graph when the denominator of k is very large? Share your findings on the discussion board.

84. Graph $f(x)=\sqrt{x}$ and $g(x)=-\sqrt{x}$ on the same set of coordinate axes. What does the general shape look like? Try to find a single equation that describes the shape. Share your findings.

85. Explore what happens to the graph of a function when the domain values are multiplied by a factor a before the function is applied, $f(ax).$ Develop some rules for this situation and share them on the discussion board.

Answers

1. e

3. d

5. f

7. 

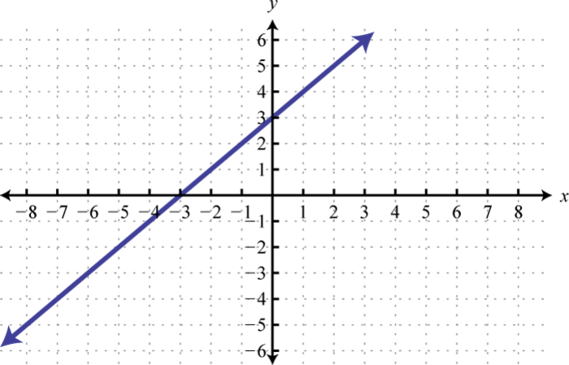
   $y=x$ ; Shift up 3 units; domain: $ℝ$ ; range: $ℝ$

9. 

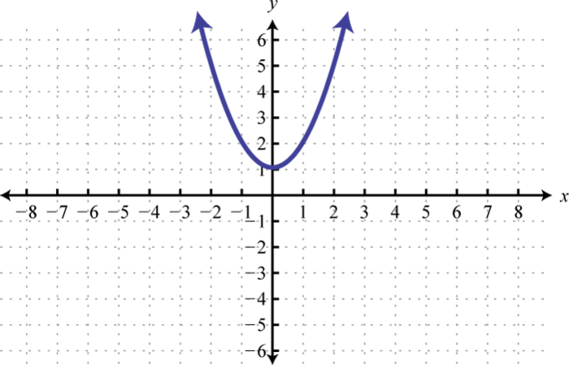
   $y=x^2$ ; Shift up 1 unit; domain: $ℝ$ ; range: $[1,\infty )$

11. 

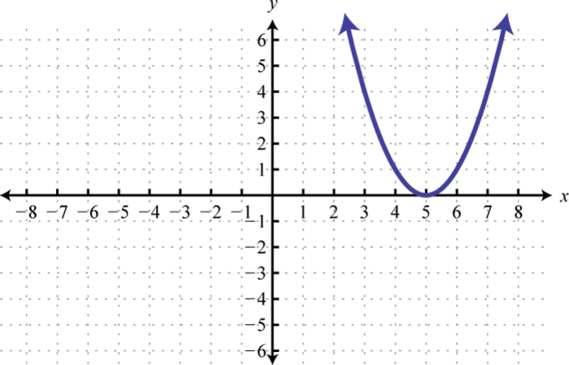
    $y=x^2$ ; Shift right 5 units; domain: $ℝ$ ; range: $[0,\infty )$

13. 

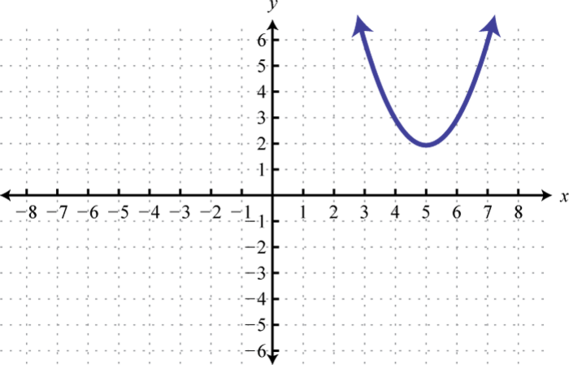
    $y=x^2$ ; Shift right 5 units and up 2 units; domain: $ℝ$ ; range: $[2,\infty )$

15. 

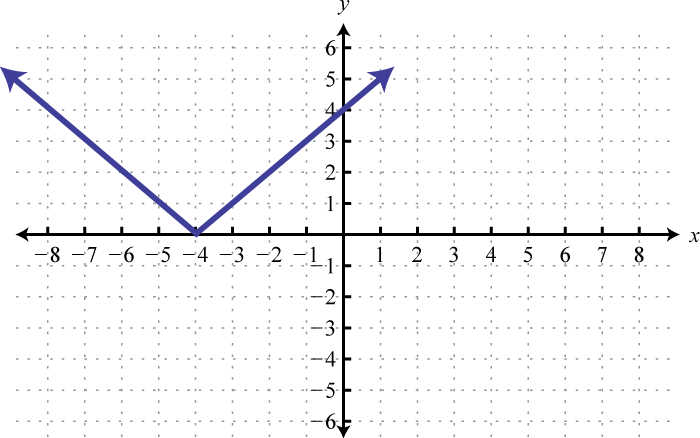
    $y=\left|x\right|$ ; Shift left 4 units; domain: $ℝ$ ; range: $[0,\infty )$

17. 

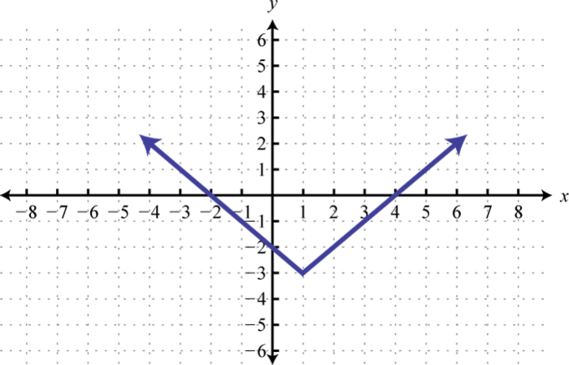
    $y=\left|x\right|$ ; Shift right 1 unit and down 3 units; domain: $ℝ$ ; range: $[-3,\infty )$

19. 

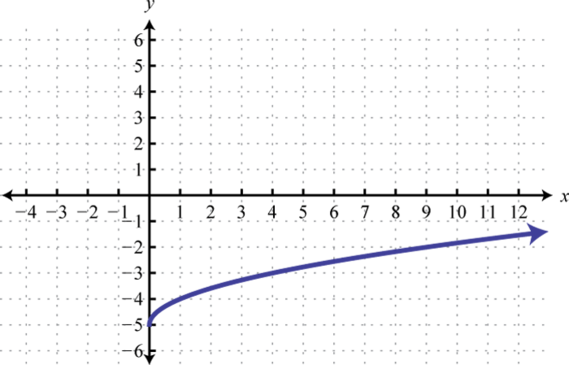
    $y=\sqrt{x}$ ; Shift down 5 units; domain: $[0,\infty )$ ; range: $[-5,\infty )$

21. 

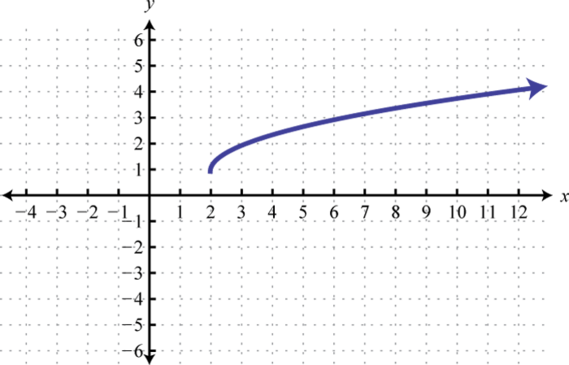
    $y=\sqrt{x}$ ; Shift right 2 units and up 1 unit; domain: $[2,\infty )$ ; range: $[1,\infty )$

23. 

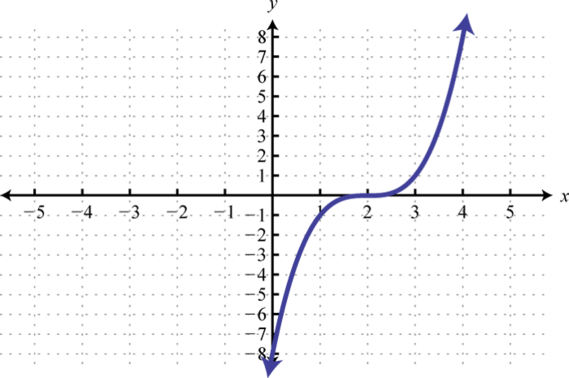
    $y=x^3$ ; Shift right 2 units; domain: $ℝ$ ; range: $ℝ$

25. 

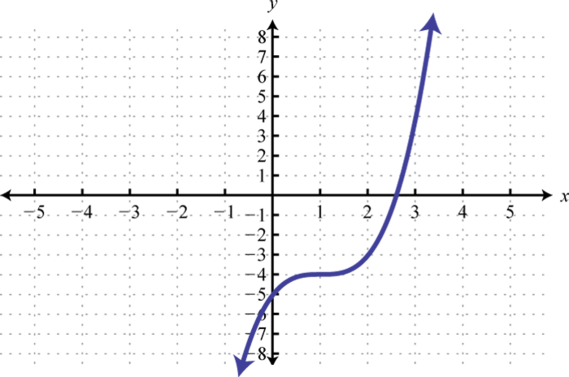
    $y=x^3$ ; Shift right 1 unit and down 4 units; domain: $ℝ$ ; range: $ℝ$

27. 

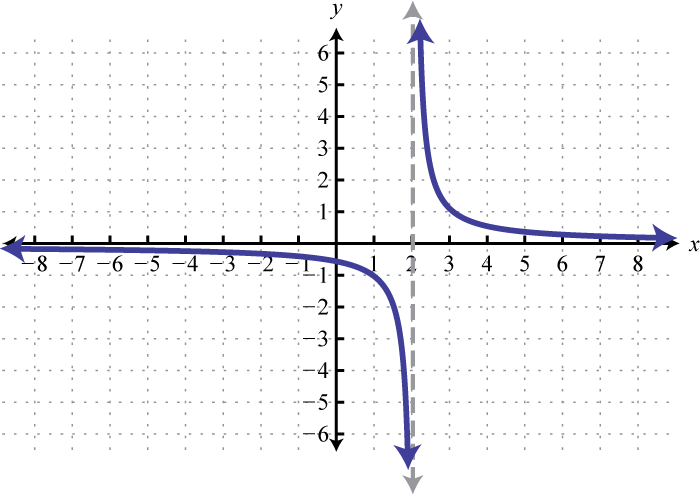
    $y=\frac{1}{x}$ ; Shift right 2 units; domain: $(-\infty ,2)\cup (2,\infty )$ ; range: $(-\infty ,0)\cup (0,\infty )$

29. 

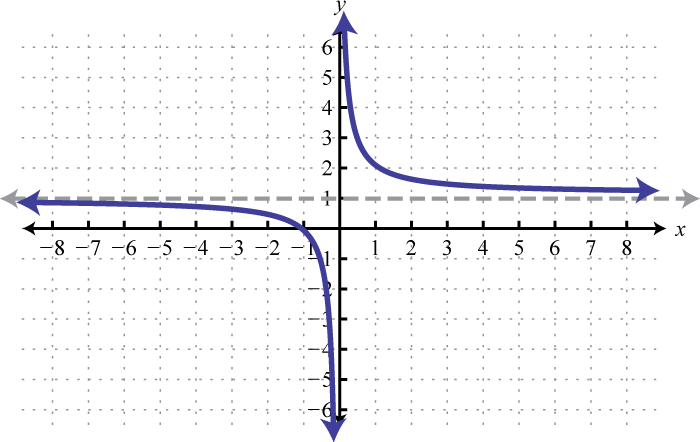
    $y=\frac{1}{x}$ ; Shift up 5 units; domain: $(-\infty ,0)\cup (0,\infty )$ ; range: $(-\infty ,1)\cup (1,\infty )$

31. 

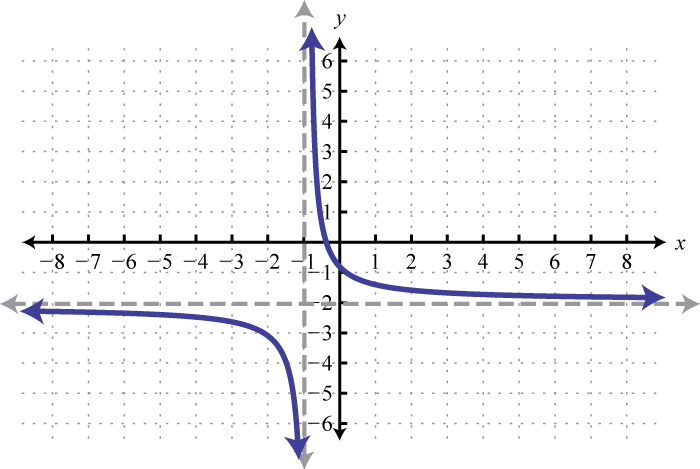
    $y=\frac{1}{x}$ ; Shift left 1 unit and down 2 units; domain: $(-\infty ,-1)\cup (-1,\infty )$ ; range: $(-\infty ,-2)\cup (-2,\infty )$

33. 

    Basic graph $y=-4$ ; domain: $ℝ$ ; range: {−4}

35. 

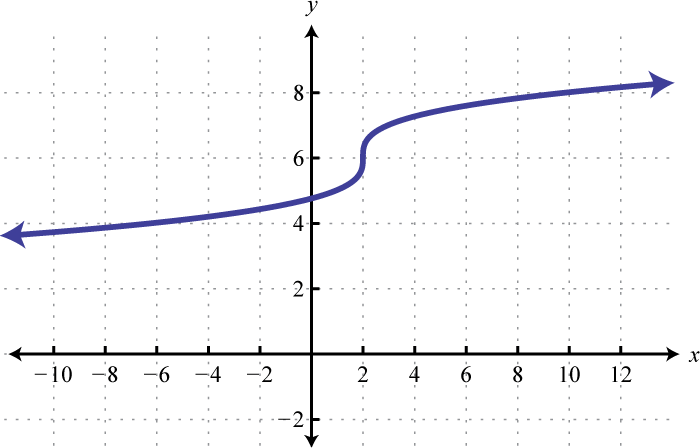
    $y=\sqrt[3]{x}$ ; Shift up 6 units and right 2 units; domain: $ℝ$ ; range: $ℝ$

37. 

39. 

41. 

43. 

45. $f(x)=\sqrt{x-5}$

47. $f(x)={(x-15)}^2-10$

49. $f(x)=\frac{1}{x+8}+4$

51. $f(x)=\sqrt{x+16}-4$

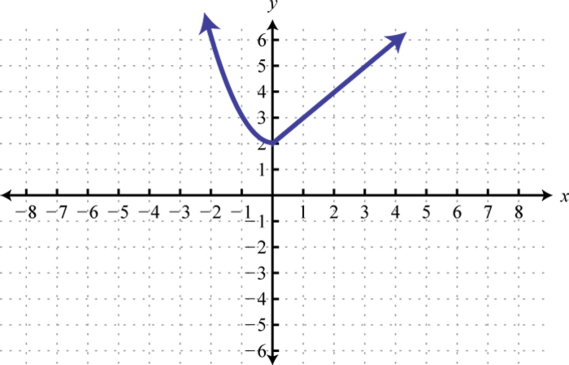
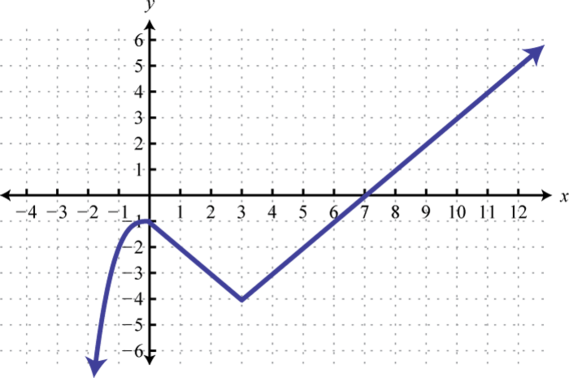
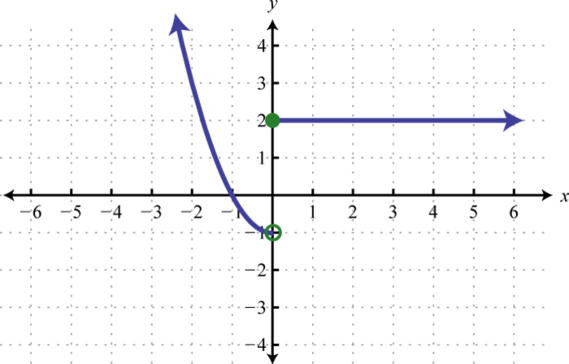
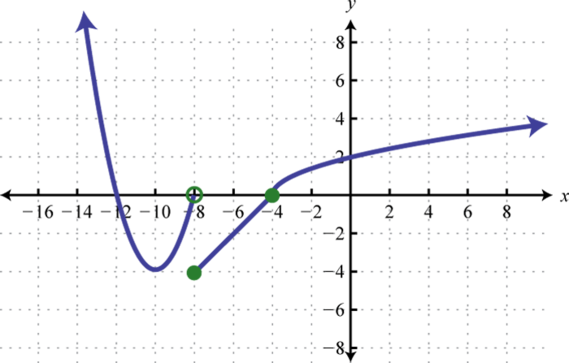
53. b

55. d

57. f

59. 

61. 

63. 

65. 

67. 

69. 

71. 

73. 

75. 

77. 

79. 

81. 

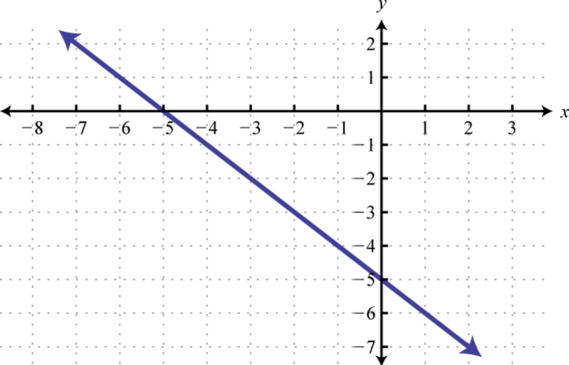
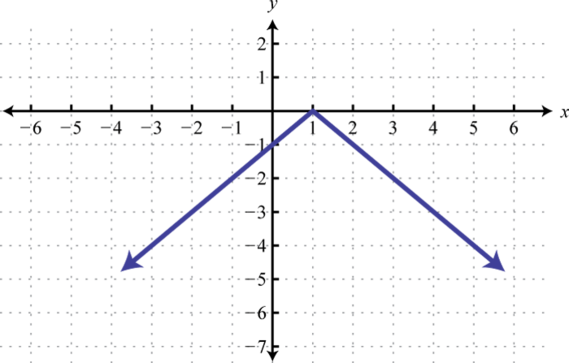
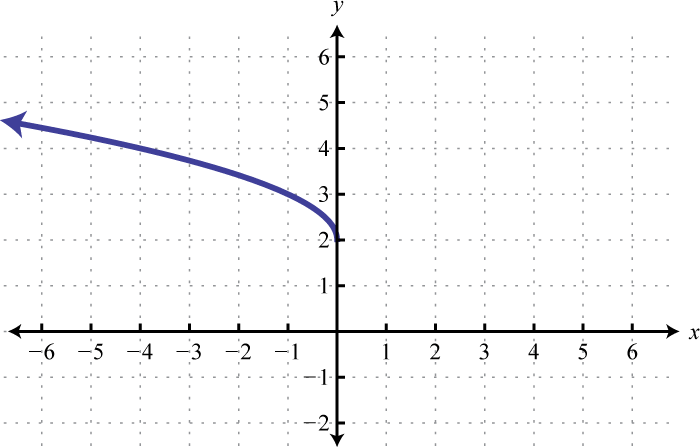
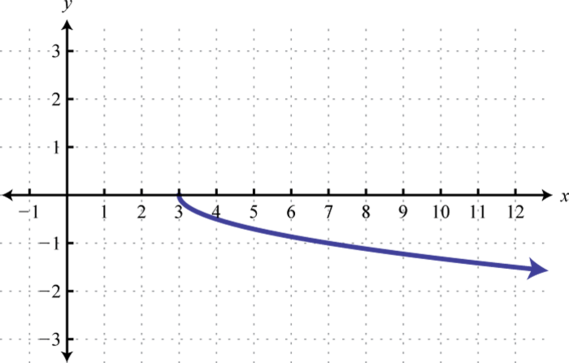
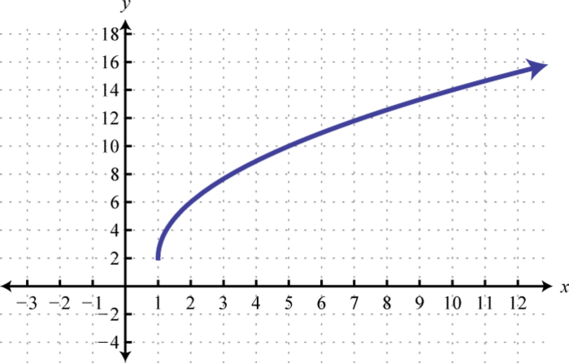
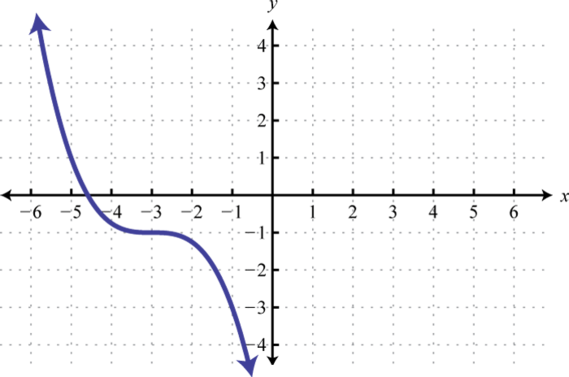
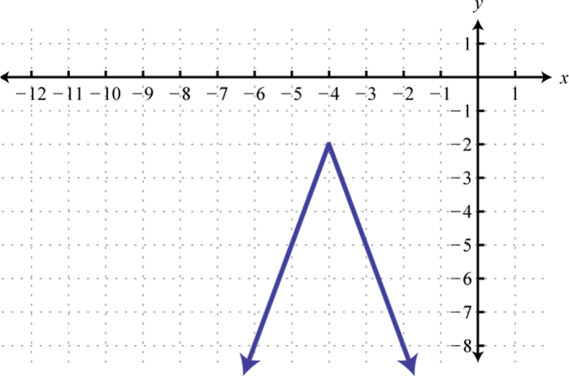
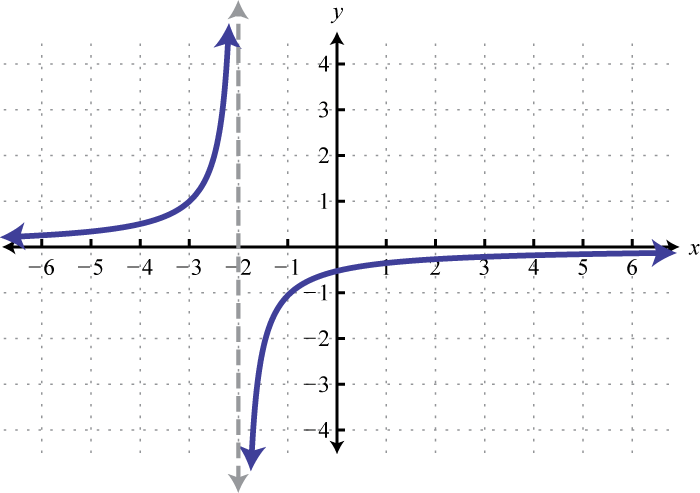
83. Answer may vary

85. Answer may vary

How to Write an Equation for a Graph Parent Functions

Source: https://saylordotorg.github.io/text_intermediate-algebra/s05-05-using-transformations-to-graph.html

Share this post